Формула полной вероятности

Следствием теоремы сложения вероятностей и теоремы умножения вероятностей является формула полной вероятнос­ти. Допустим: дана совокупность несовместных, образующих полную группу событий Ии Я2, …. Ип. Некоторое событие А может произойти только вместе с одним нз этих событий. Тре­буется найти вероятность события А.

Доказательство. Так как события И и Я2, …, Нп nf)разуют полную группу, то событие А и сложное событие //і + Я2+… + Ип соединены союзом «если А, то Яі + Я2 + К..+ Нп » и «если И + И2+. -.+Я„, то А». Эти соотношения можно записать в такой форме: А -*• Яі+Я2-Ь.. . + ЯЛ и на — 1 іборот Яі+Я2+.-.+Ял->А Следовательно,

А =Я1 + Яа+…+ЯЛ. (2.5)

і множив обе части равенства (2.5) на А, получим А — А • Нг + А’ Н2 — Ь… + A’Hni

P{A)^±P{A-Hl)=fiP (Я,) Я (Л/Я,). (2.6)

/«і

Отказ системы может иметь место, когда откажет хотя бы один из элементов системы (при одиночном соединении). По — этому вероятность отказа системы может быть рассчитана по формуле (2.6).

Пример 2.4. Для условий примера 2.1 известно, что веро­ятности безотказной работы первого элемента P(3i) и второ­го элемента Р(Э2) соответственно равны Р(Э|) =0,8- Р(Э2) = =0,9.

Требуется определить:

Q (С/Э, Э2) — вероятность отказа системы при условии

отказа первого элемента и работоспособ­ности второго элемента;

Q (CJBj Э,) — вероятность отказа системы при условии

работоспособности первого элемента и от­каза второго элемента;

Q (С/Э1Э2) —• вероятность отказа системы при условии

отказов первого н второго элементов;

Решение. 1. Согласно формуле (2.2) определяем веро­ятности отказа первого и второго элементов;

Q (Э,) — I — Я(Э,) — 1 — 0,8 = 0,2:

Q (Э2) — 1 Я(Э2) = 1 — 0,9 = 0,1.

2. Согласно формуле (2.4) определяем вероятности отказа системы при условии отказа первого элемента, отказа систе­мы при условии отказа второго элемента и отказа системы при условии отказов первого и второго элементов:

Q (С/Э, Эе) = Q (Эх) Я (Э*) = 0,2 — 0,9 — 0,18;

Q (С/ЭХЭ2) = PO,)Q(9a) = 0,8-0,1 = 0,08;

Q(C/9, Эа) = Q(3,)Q(32) = 0,2-0,1 -0,02.

Пример 2.5. На рис. 2.3 изображена сложная система эле­ментов. Элементы / и 4 соединены между собою одиночно и образуют подсистему 1—4. Элементы 3 и 5 также соедине­ны одиночно и образуют подсистему 3—5. Подсистемы 1—4 и 3—5 соединены между собою резервно. Элемент 2 одиночно соединен как с элементом 4, так и с элементом 5.

Требуется рассчитать вероятность безотказной работы всей системы Рс — Я (С) = ?

Вероятности безотказной работы элементов известны и равны P(3j)=p,; Р(Э2)=р2; Р(Э3)=р3; Р(Э4)=р4; Р(Э5) =ps-

Решение. 1. Согласно формуле (2.6) определяем вероят­ное 1Ъ отказа системы:

Qc = Q(C/32)/72 + Q(C/9k)ft,

3. Окончательно вероятность безотказной работы системы Рс будет равна

Яс — 1 — Qc ~ 1 — тС1Э2)р2 + Q(C/3a)( 1 — р*)].

2.4. Теорема гипотез (формула Бейеса)

Следствием теоремы умножения и формулы полной веро­ятности является теорема гипотез или формула Бейеса. Эта теорема используется в теории надежности для разработки оптимальной последовательности поиска отказавших элемен­тов.

Постановка задачи.

Дана полная группа несовместных гипотез Я2, Я3, . Ип. Вероятности этих гипотез известны до опыта и соответ­ственно равны

РШ Р(И2), рт, …. Р{НП).

Произведен опыт, в результате которого наблюдалось собы­тие А. Спрашивается, как следует изменить вероятности гипо­тез в связи с появлением этого события? По существу задачи требуется определить условные вероятности гипотез tit в связи с этим событием А Иными словами, требуется опреде­лить условные вероятности гипотез P(Ht IA), вычисленные при условии события А.

Согласно формуле (2.3) имеем

Р (А) Р {Иі! А) = Р (Я,) Р [АІЩ.

Используя формулу (2.6), получаем

rtH « РіЩРіАІН,)

Р**і’А) = ———————- .

^іР(ЩР{АіНі)

Пример 2.6. Дана система С, состоящая нз трех одиночно соединенных элементов Эь Э2, Э3. Вероятности безотказной ра­боты этих элементов pi —0,9; рг~0,8; рз—0,75. В процессе эксплуатации система будет находиться в одном и только в одном из восьми возможных состояний

Вероятности нахождения системы в каждом из восьми возможных состояний даются в табл. 2.1.

Таблица 2.1 Hi ~ /* (Я/) N Переоценка после проверки с резуль­татом С 1 РіРїР’л — 0,9-0,8-0,75 = 0,5*1 0 II (1 р)р2Р> = 0,1 -0,? *0,75 — 0,о<3 0.10 111 р,0 = 0,9.0,2*0,75— 0,135 0,36 IV PiP.2(l — Рэ) = 0,9-0,8*0,25 — 0,180 0,48 V (1 — Pi) (1 ~рй)р3 — 0,1 *0,2-0,75 — 0,015 0 VI рх (1 — р2) (1 —Рг) — 0,9-0.2-0,25 — 0,045 О VII (1 Pi) Р‘2 (1 — р?) = 0,01 -0,8-0,25 = 0.020 0 VIU (1 — Рх) (I — р2) (1 —— Рз) = 0.1 -0.2-0,25 = 0,005 0

Проведена проверка работоспособности системы С, кото* рая показала отрицательный результат, т. е. уточнено, что си­стема в момент проверки неработоспособна. Требуется опре­делить, как изменяется вероятность нахождения системы в состояниях II, III, IV, V, VI, VII, VIII. Поскольку нахожде­ние отказавшей системы в состояниях V, VI, VII, VIII мало­вероятно (меньше пяти процентов), то ограничимся рассмот­рением только состояний II, III, IV.

До проверки возможны следующие гипотезы о возмож­ных состояниях системы: Яj — все элементы системы работо­способны; Н2—отказал первый элемент, второй и третий ра­ботоспособны; Я3— отказал второй элемент, первый и третий работоспособны; Я/— отказал третий элемент, первый и вто­рой работоспособны.

Вероятности этих гипотез: Р(Яі)=0,54; Р(Я2) =0,06;

I (Я3) =0,135; Р(Н4) =0,180.

После проверки работоспособности системы гипотеза Нх невозможна и вероятности гипотез Н2> Нз, //4 определяются согласно формуле (2.7):

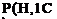тн.

ІтГ

/=і

______________ ___________________________________

(1 *f Plp2(l ~Ps)*l

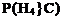___________ (1 — Pz)PiPs1_________

(1 — р,)р2Р8 + Рі(1 Pt)Ps + Pi Рі ( Рз)

0, 135

0, 375

___________ (1 — Pg)piPsl______________

(1 — Рі)Р»Рз4-Рі(1 ~Р2)Рз + Р, Р»(1 — Рз)

0, 18

0, 375

Пример 2.7. На самолетах авиационной группы установ­лены агрегаты производства трех заводов, причем агрегатов завода № 1 —20%, завода № 2 — 30% и завода № 3 — 50% • Вероятности безотказной работы агрегатов, изготовленных на заводах № 1, № 2 и № 3, соответственно равны 0,9; 0,92; 0,808.

Произошел отказ бортовой системы из-за отказа этого аг­регата. Каковы вероятности того, что отказавший агрегат про­изводства первого, второго нли третьего заводов.

Решение. 1. По условию задачи:

Р(Я0 = 0,2; Р(Я8) = 0,3; Р(Я8)-0,5;

Р(А! НХ)~ 0,9; Р{А1Щ -0,92; Р(Л/Я8) = 0,808.

По формуле полной вероятности (2.6) вычисляем вероят­ность безотказной работы агрегатов данного типа:

Р(А) = 0,2-0,9 4- 0,3-0,92 + 0,5*0,808 = 0,86.

2. Вычисляем вероятность отказа агрегатов данного типа:

Я(А} = 1 — 0,86 =*0,14.

3. По формуле Бейса (2.7) вычисляем вероятности того, что отказавший агрегат производства первого, второго или третьего заводов:

Р(Н, ГЛ)= =- 0,143;